阅读笔记-High-speed tracking with kernelized correlation filters

Abstract

​ KCF是一种鉴别式追踪方法，这类方法一般都是在追踪过程中训练一个目标检测器，使用目标检测器去检测下一帧预测位置是否是目标，然后再使用新检测结果去更新训练集进而更新目标检测器。而在训练目标检测器时一般选取目标区域为正样本，目标的周围区域为负样本，当然越靠近目标的区域分为正样本的概率越高。

​ 本篇博文希望借这篇文章阐述KCF的原理和过程，以及存在的一些问题。

原发表于博客园

---

Notations

​ 论文中关于向量是行向量还是列向量总是指示不清楚，所以本文对变量符号统一之后进行推导，首先所有的小写字母均表示列向量，所有的大写字母表示矩阵，其中矩阵的每一行是一个样本，文中的函数除了$\phi(h)$是对行向量操作，其余都是对元素操做的，四则运算符号也都是针对元素操作的。还有所有对循环矩阵使用傅里叶变换时使用的生成向量都是循环矩阵的第一行向量，这点很重要。

Contributions

• 使用目标周围区域的循环矩阵采集正负样本，利用脊回归训练目标检测器，并成功的利用循环矩阵在傅里叶空间可对角化的性质将矩阵的运算转化为向量的Hadamad积，即元素的点乘，大大降低了运算量，提高了运算速度，使算法满足实时性要求。
• 将线性空间的脊回归通过核函数映射到非线性空间，在非线性空间通过求解一个对偶问题和某些常见的约束，同样的可以使用循环矩阵傅里叶空间对角化简化计算。
• 给出了一种将多通道数据融入该算法的途径。

---

Inference

一维脊回归

给定训练集$(x_i, y_i)， x_i\in R^{1\times n}, y_i\in R$, 其线性回归函数表示为$f(x_i) = w^Tx_i$, 回归系数$w\in R^{n\times 1}$ 可以通过最小二乘法计算：

$$w^* = \min_w\sum_i(f(x_i)-y_i)^2 + \lambda \Vert w\Vert^2$$

$\lambda$是正则化系数， 限制模型的VC维从而保证模型泛化性能。

其矩阵形式表示为:

$$w^* = \min_w \Vert Xw - y\Vert^2 +\lambda \Vert w\Vert^2$$

$X=[x_1, x_2, …,x_n]^T$.

采用最小二乘法求解，可得：

$$w^* = (X^TX + \lambda I)^{-1}X^Ty$$

将模型扩展到复数空间，即：

$$w^* = (X^HX+\lambda I)^{-1}X^Hy$$

$X^H$是$X$的复共轭矩阵。

循环矩阵

KCF中 训练样本是由目标样本经过循环位移得到。向量的循环可以使用排列矩阵获得, 下式中$P, Q$分别表示循环右移和左移矩阵：

$$x_i = [x_{i1}, x_{i2},\dots x_{in}]^T\\ P = \left[ \begin{array}{ccccc} 0, 0, \cdots, 0, 1\\ 1, 0, \cdots, 0, 0\\ 0, 1, \cdots, 0, 0\\ ...\\ 0, 0, \cdots, 1, 0 \end{array} \right],~~~~ Q= P^T\\ Px_i = [x_{in}, x_{i1},\dots x_{i(n-1)}]^T\\ x_iQ = [ x_{i2},\dots x_{in}, x_{i1}]^T$$

因此样本向量经过不断的左乘或者右乘排列矩阵，就可以实现循环位移，多个循环结果按序stack就成为循环矩阵$C(x)$如下图：

​ 1D 循环矩阵示意

​ 2D 图像循环示例

循环矩阵傅氏空间对角化

所有循环矩阵$C(x)$都能够在傅氏空间中使用离散傅里叶变换进行对角化

$$X = C(x) = F \cdot \text{diag}(\hat{x}) \cdot F^H$$

x是循环矩阵的生成向量，即对应于$C(x)$的第一行。 $\hat{x} = \mathcal{F}(x) =\sqrt{n}Fx$是$x$的傅里叶变换， $F$是傅里叶变换矩阵，常量：

$$F=\frac{1}{\sqrt{n}} \left[ \begin{array}{lllll} 1,~~~~1,~~~\cdots,~~~~~~~1, ~~~~1\\ 1,~~~ w, ~~~\cdots, ~~~~~w^{n-2}, w^{n-1}\\ ~~~~~~~~~~~~\cdots \\ 1, w^{n-1}, \cdots, w^{(n-1)(n-2)}, w^{(n-1)^2} \end{array} \right]$$

关于矩阵傅里叶对角化请参考循环矩阵傅里叶对角化., $F$是酉矩阵， 即$FF^H=F^HF=I$

傅氏对角化简化的脊回归

将$X=F\text{diag}(\hat{x})F^H$代入公式(4).

$$\begin{align} w & = (F\cdot\text{diag}(\hat{x}^*)\cdot F^HF\cdot \text{diag}(\hat{x})\cdot F^H + \lambda F^HF)^{-1}F\cdot \text{diag}(\hat{x}^*)\cdot F^Hy \\ &= (F\cdot\text{diag}(\hat{x}^*\odot\hat{x}+\lambda)\cdot F^H)^{-1}F\cdot\text{diag}(\hat{x}^*)F^Hy\\ &= F\cdot \text{diag}(\frac{\hat{x}^*}{\hat{x}^*\odot\hat{x}+\lambda})\cdot F^Hy \end{align}$$

有公式(6)可以进一步得到：

$$\begin{align} w &= C(F^{-1}(\frac{\hat{x}^*}{\hat{x}^*\odot\hat{x}+\lambda}))y \\ \hat{w}&=\mathcal{F}^*(F^{-1}(\frac{\hat{x}^*}{\hat{x}^*\odot\hat{x}+\lambda})) \odot \mathcal{F}(y)\\ &= \frac{\hat{x}\odot \hat{y}}{\hat{x}^*\odot\hat{x}+\lambda}\\ w &= \mathcal{F}^{-1}(\hat{w}) \end{align}$$

这是因为$\mathcal{F}(C(x)y) = \mathcal{F}^*(x)\odot \mathcal{F}(y)$

于是可以使用向量点积代替矩阵运算，特别是牵涉到矩阵求逆运算。

核空间的脊回归

我们希望将样本数据映射到非线性空间内再进行回归，以期待新的空间内可分。于是新空间内回归函数为$f(x_i)=w^T\phi(x)$, 其中$\phi(\cdot)$是核函数。于是 $w = \min_w \Vert(\phi(X)w - y)\Vert^2 +\lambda \Vert w\Vert^2$

理想情形$w$是$\phi(X)w - y$零空间的向量，所以$w$可以由$\phi(X)=[\phi(x_1, x_2, \cdots, x_n)]^T$线性表示，于是$w=\sum_i \alpha_i\phi(x_i)=\phi(X)^T\alpha$, 于是

$$\alpha = \min_a \Vert \phi(X)\phi(X)^T\alpha - y\Vert^2 + \lambda\Vert \phi(X)^T\alpha\Vert^2$$

该问题是$w$的对偶问题。

对$\alpha$计算导数并令其为0， 得到

$$\begin{align} J(\alpha) &= \alpha^T \phi(X)\phi(X)^T\phi(X)\phi(X)^T\alpha - 2y^T\phi(X)\phi(X)^T\alpha +C_{constant} + \lambda \alpha^T\phi(X)\phi(X)^T\alpha \\ &= 2\phi(X)\phi(X)^T\phi(X)\phi(X)^T\alpha + 2\lambda \phi(X)\phi(X)^T\alpha - 2\phi(X)\phi(X)^Ty = 0\\ \bar{\alpha} &= (\phi(X)\phi(X)^T+\lambda I)^{-1}y \end{align}$$

此处推导用到$\phi(X)\phi(X)^T$是协方差矩阵一定可逆的知识。

核方法中我们不知道核函数$\phi(\cdot)$的具体形式，但可以构造核矩阵$K=\phi(X)\phi(X)^T$, 于是$\bar{\alpha} = (K+\lambda I)^{-1}y$

$$f(z) = w^T\phi(z) = \alpha^T\phi(X)\phi(z)$$

如果希望计算$\alpha $也可以利用傅氏空间对角化知识，那么$K$是一个循环位移矩阵。

Theorem 1. Given circulant data $C(x)$, the corresponding kernel matrix $K$ is circulatant if the kernel function satisfies $K(x, x’) = K(Mx, Mx’)$,for any permutation matrix $M$.
即核矩阵是循环矩阵应该满足两个条件：第一个样本和第二个样本都是由生成样本循环移位产生的，可以不是由同一个样本生成；满足$K(x, x’) = K(Mx, Mx’)$,其中$M$是排列矩阵。

证明： 设$x\in R^n$, 则其生成向量$x’ = P^ix, \forall x’\in C(x)$, 于是：

$$\begin{align} K_{ij} &= \phi(x_i)^T\phi(x_j)\\ &= K(x_i, x_j)\\ &= K(P^ix, P^jx) \\ &= K(P^{-i}P^ix, P^{-i}P^{j}x), ~~\text{cause}~~ K(x, x')=K(Mx, Mx')\\ &= K(x, P^{j-i}x) \\ &= \phi(x)^T\phi(P^{j-i}x) \\ &= \phi(x)^T\phi(x_{j-i}) \end{align}$$

从而

$$K_{0\cdot} = [\phi(x_0)^T\phi(x_0), \phi(x_0)^T\phi(x_1), ..., \phi(x_0)^T\phi(x_{n-1})]\\ K_{1\cdot} = [\phi(x_0)^T\phi(x_{n-1}), \phi(x_0)^T\phi(x_0), ..., \phi(x_0)^T\phi(x_{n-2})]$$

这里，$j-i$表示位移数目， 负数表示左移数目。

因此可以证明Theorem1。

所以，只要选取核函数满足$K(x,x’)=K(Mx, Mx’)$， 那么核矩阵就是循环矩阵。当核矩阵是循环矩阵时，

$$\begin{align} \alpha &= F\cdot \text{diag}(\hat{K}^{xx}+\lambda)^-1\cdot F y\\ \hat{\alpha} &= \frac{\hat{y}}{(\hat{K}^{xx}+\lambda)^*}\\ &= \frac{\hat{y}}{(\hat{K}^{xx}+\lambda)} \end{align}$$

其中$K^{xx}=\phi(x)^T\phi(X)^T$是核矩阵的生成向量，也是矩阵的第一行。

注意，核函数一般满足对称性，即$K(x,y)=K(y,x)$, 于是可以证明$K^{xx}$是对称向量，即$K^{xx}_{0i} = K^{xx}_{0(n-i)}$, 对称向量的傅里叶变换为实数，因此其共轭可以忽略

满足上述性质的核函数包括：

• Radial Basis Function kernels -e.g. Gaussian
• Dot-Product kernels -e.g. linear, polynomial
• Additive kernels - e.g. intersection, $\chi^2$ and Hellinger kernels
• Exponentiated additive kernels.

快速检测

首先由训练样本和标签训练检测器，其中训练集是由目标区域和由其移位得到的若干样本组成，对应的标签是根据距离越近正样本可能性越大的准则赋值的，于是得到训练样本集和对应的标签，采用上一节的核空间回归，可以计算得到$\alpha$

在检测样本时，认为待检测样本是target位移得到的，即$z_j = P^jz$, 于是其对应的回归值为$f(z_j) = \alpha^T\phi(X)\phi(z_j)$, 回归值最大则表明最可能是目标。

定义核矩阵$K^z= \phi(X)\phi(Z)^T$, 即 $K_{ij}^z = \phi(z_i)^T\phi(x_j)$, 由定理1可确定$K^z$是循环矩阵。

于是在检测时，每个测试样本的回归值如下计算：

$$\begin{align} f(z) &= (\alpha^T\phi(X)\phi(Z)^T)^T\\ &= (K^z)^T\alpha\\ &= F\cdot \text{diag}(\hat{x}^{xz})\cdot F^H\alpha\\ \hat{f}(z) &= (\hat{K}^{xz})^*\hat{\alpha} \end{align}$$

$K^{zx}$是$K^z$的生成向量。

核矩阵的快速计算

目前计算瓶颈还有核矩阵的生成向量的计算。

内积和多项式核

即$K(x_i, x_j’) = g(x_i^Tx_j’)$于是

$$\begin{align} K^{xx'} &= g(C(x)x')^T \\ &= g(\mathcal{F}^{-1}(\hat{x}^*\odot \hat{x}''))^T \end{align}$$

因此对于多项式核$K(x_i, x_j) = (x_i^Tx_j + a)^b$有

$$K^{xx'} =((\mathcal{F}^{-1}(\hat{x}^*\odot \hat{x}''))^T+a)^b$$

径向基核函数

这类核函数重点在于计算$\Vert x_i-x_j\Vert^2$

$\Vert x_i-x_j\Vert^2 = \Vert x_i\Vert^2 + \Vert x_j\Vert^2 - 2 x_i^Tx_j$

所以

$$K^{xx'} = h(\Vert x\Vert^2 + \Vert x' \Vert^2 -2\mathcal{F}^{-1}(\hat{x}^*\odot \hat{x}'))^T$$

对于高斯核有：

$$K^{xx'} = exp(\frac{1}{\sigma^2}\Vert x\Vert^2 + \Vert x' \Vert^2 -2\mathcal{F}^{-1}(\hat{x}^*\odot \hat{x}'))^T$$

1D to 2D

2D数据时可以直接在核空间使用傅里叶变换对角化循环矩阵的特征，加速运算。

现有一个核函数$\varphi(\cdot)$, 自变量$X_i\in R^{m\times n}$, 于是$\varphi(X_i)\in R^k$, 于是核空间采用脊回归公式

$$\alpha = (K+\lambda I)^{-1}y$$

Theorem 2. The block matrix $K$ with elements $K_{(ii’)(jj’)} = \mathcal{K}(P^iXP^{i’}, P^jXP^{j’})$ is a Block-Circulant Matrix if $\mathcal{K}$ is a unitary invariant kernel.

Here, unitary invariant kernel satisfies $\mathcal{K}(X, X’) = \mathcal{K}(P^iXP^{i’}, P^iX’P^{i’})$

块循环矩阵可以使用2D傅里叶变换实现矩阵对角化

$$K = F_2\cdot \text{diag}(\hat{K}')\cdot F_2^H$$

其中$F_2$是2D傅里叶变换矩阵， $K’$是生成块循环矩阵的生成矩阵， $\hat{K}$表示对矩阵$K$进行2D傅里叶变换。

于是

$$\alpha = F_2\cdot (\text{diag}(\hat{K}'+\lambda 1^m(1^n)^T))\cdot F_2^Hy$$

其中$1^m, 1^n$表示全1向量。

由公式6可得：

$$\hat{\alpha}_M = (\hat{K}'+\lambda 1^m(1^n)^T)*\odot \hat{y}_M$$

$\alpha_M, y_M$分别表示矩阵形式的系数和标签。

于是回归值为

$$\hat{f}_M = \hat{K}^{XZ}\odot \hat\alpha_M$$

其中$K^{XZ}$表示块循环矩阵的生成矩阵。

再往后的检测部分与1D类似，不作赘述。

多通道问题

论文中在提取目标区域的特征时可以是灰度特征，但是使用Hog特征能够取得更好的效果，那么Hog特征该如何加入前面提到的模型呢？

Hog特征是将图像划分成较小的局部块，称为cell，在cell里提取梯度信息，绘制梯度方向直方图，然后为了减小光照影响，将几个cell的方向直方图串在一起进行block归一化，最终将所有的cell直方图串联起来就是图像的特征啦。

那么，按照传统的方式一张图像就提取出一个向量，但是这个向量怎么用啊？我们又不能通过该向量的移位来获得采样样本，因为，你想啊，把直方图的一个bin循环移位有什么意义啊？

所以论文中Hog特征的提取是将sample区域划分成若干的区域，然后再每个区域提取特征，代码中是在每个区域提取了32维特征，即划分9个梯度方向， 每个防线提取3个特征，然后再加上4个表观纹理特征和一个0元素表示阶段特征，详情参考FHOG. 共 $3x9+5=32$维特征，于是可以使用$m\times n \times 32$表示图像，其中$m,n$是划分区域的网格数。那么这么操作之后矩阵为位移可以近似于patch块的位移，也就是网格的位移，于是矩阵的循环位移就是网格特征$m\times n \times 31$的每一通道上的循环位移，这里最后一维特征全0不考虑。

Conclusion

• KCF相对于以前的单目标跟踪方法速度提升明显，性能也较好，思路简单。

  

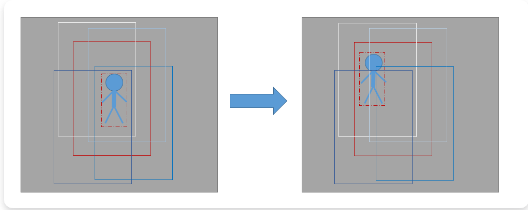
  ​ KCF example

借上图来总结下KCF的过程，左图是刚开始我们使用红色虚线框框定了目标，然后红色实线框就是使用的padding了，其他的框就是将padding循环移位之后对齐目标得到的样本，由这些样本就可以训练出一个分类器，当分类器设计好之后，来到了下一帧图像，也就是右图，这时候我们首先在预测区域也就是红色实线框区域采样，然后对该采样进行循环移位，对齐目标后就像图中显示的那个样子 了，（这是为了理解，实际中不用对齐。。。），就是周围那些框框啦，使用分类器对这些框框计算响应，显然这时候白色框响应最大，因为他和之前一帧红色框一样，那我们通过白色框的相对移位就能推测目标的位移了。然后继续，再训练再检测。。。。

论文中还提到几点：

1. 对特征图像进行cosine window加权，这主要是为了减轻由于边界移位导致图像不光滑。
2. padding的size是目标框的2.5倍，肯定要使用padding窗口，要不然移位一次目标就被分解重组合了。。。效果能好哪去。。
3. 对于标签使用了高斯加权。 这点尤其重要。
4. 对$\alpha$前后帧结果进行了线性插值，为了让他长记性，不至于模型剧烈变化。

• KCF的不足点
  1. 依赖循环矩阵，对于多尺度的目标跟踪效果并不理想。当然可以通过设置多个size，在每个size上进行KCF运算，但这样的话很难确定应预先设置多少size，什么样的size，而且对size的遍历必将影响算法的速度。KCF最大的优势就是速度。
  2. 初始化矩阵不能自适应改变，其实这个问题和上一个缺点类似，这里强调的是非刚体运动，比如跳水运动员，刚开始选定区域肯定是个瘦长的矩形框，但当运动员开始屈体的时候显然这个预选定框就很大误差了。
  3. 难处理高速运动的目标， 高速运动目标很容易超出候选区域。
  4. 难处理低帧率中目标，这个和3类似，都是说相邻帧间目标位移过大。