多目标跟踪总结(上)-传统方法

导言

参考SIGAI公众号推文，欢迎关注SIGAI公众号。

目标跟踪是计算机视觉中的一个重要任务。在计算机视觉的三层结构中，目标跟踪属于中间层，是其他高层任务，如动作识别、行为分析等，的基础。其广泛应用于视频监控，人机交互，自动驾驶，医学图像，虚拟现实和增强现实等现实场景中。目标跟踪根据每帧跟踪目标个数不同又划分为单目标跟踪(Single Object Tracking, SOT)和多目标跟踪(Multiple Object Tracking, MOT)。

单目标跟踪任务在图像序列第一帧中采用bounding box或者其他方式标定待跟踪目标，然后利用跟踪算法在之后帧中逐步确定该目标在每一帧的位置。单目标跟踪场景中一般会遇到物体形变，背景干扰，偶然遮挡等因素。

多目标跟踪任务是在图像序列的每一帧中同时确定目标的位置和身份，即轨迹ID。MOT任务除了会遇到单目标场景中的物体形变，背景干扰等因素，还具有一些独特的更复杂的问题。

待跟踪目标如何处理目标的出现和消失。MOT任务中，目标是可以在任意时刻出现或者消失在视野中的。
如何鉴别不同的个体。MOT任务中有时多个目标来源于同一类别，比如行人跟踪，他们具有相似的表观和轮廓，如何区分他们是降低ID switch，提升性能的关键。
跟踪目标之间的交互与遮挡。MOT任务中目标个数较多，交互复杂，特别是拥挤场景中相互遮挡严重，如何解决相互遮挡是保障跟踪顺利的关键。
目标重出现时如何重识别。当目标长时间被遮挡后再次出现，如何正确的找回原来的轨迹编号也是个难题。

多目标跟踪任务中出现的一些术语：

目标：在图像中，明显区别于周围环境的闭合区域往往被称为目标，这些目标一般是一些感兴趣区域ROI。
检测：通过算法得到目标在图像中的位置的过程称为检测。近些年检测器的发展非常迅速，从最初的模板匹配到目前流行的深度学习方法，比如Faster RCNN系列， SSD系列， YOLO系列， CornerNet系列等。检测器的性能得到极大的提升。
跟踪：不同帧中，物理意义下的同一目标相关联的过程
检测响应：检测过程的输出量，即检测结果。在不引起混淆的环境中，也用‘检测’表示检测响应。
跟踪假设：每一帧中跟踪的结果。
轨迹：MOT系统的输出量，一条轨迹对应这一个目标在一个时间段内中的位置序列。
轨迹片段：完整轨迹中的一些连贯的较短的轨迹碎片。
数据关联：目标之间的匹配。MOT任务中在数据关联阶段一般假设一条轨迹只能对应一个检测响应，同时一个检测响应最多对应一条轨迹。

这篇文章简单介绍和归纳一些经典的多目标跟踪方法。

多目标跟踪算法分类

多目标跟踪问题最早提出是在雷达信号中同时跟踪多架敌机和多枚导弹。这些算法后来被借鉴用于机器视觉领域的多目标跟踪任务。多目标跟踪算法分类不是很严格，根据不同的分类标准有不同的分类方法。比如

按目标初始化方式的不同划分为Detection Based Tracking (DBT)和Detection Free Tracking (DFT)。

DFT需要在目标出现的第一帧中标定目标位置，之后跟踪中边检测目标边跟踪目标。DBT是将MOT任务划分为两个阶段：Detection + Data Association. 随着检测器性能的大幅提升，基于检测的多目标跟踪算法是目前主流的跟踪算法。
按目标处理过程中用到的信息范围划分为在线跟踪和离线跟踪。

离线跟踪需要用到当前时刻之前和之后的信息，利用这些特征构建图，网络流等复杂的模型，然后跟踪当前时刻目标，这类方法能够很好的解决遮挡问题，一般性能较好。但是其明显的不足点在于很难适应实时跟踪的需求。在线跟踪则要求对当前时刻的检测响应进行跟踪是只能利用之前和当前的信息，该类算法的难点在于处理遮挡和检测的不准确问题。
按跟踪算法的表示形式和优化框架划分为确定性推导和概率统计最大化两类。

确定性推导是将检测和已跟踪的轨迹看做二元变量，通过构建整体的目标函数，计算最佳匹配，比如经典的二部图分配等。概率统计最大化方法是将检测和轨迹的关系通过概率模型表示，然后通过最大化该概率模型计算最优分配，比如基于贝叶斯的Kalman 滤波和粒子滤波，马尔科夫链等。
按应用角度不同可分为运动场景、航拍场景等。

运动场景，比如运动员的跟踪。运动场中同一队伍的队员队服几乎相同，并且运动场景图像角度，尺寸变化较大给跟踪带来很大困难，当然运动场景中一些先验假设比如场地边缘等信息给目标跟踪带来一定帮助。航拍场景中目标往往太小，帧率太低，位移太大，较难处理。这类方法主要依靠上下文信息解决。

一般而言，MOT的不同分类是存在重叠的。MOT的分类只是提供了不同角度理解跟踪算法，对算法本身并没有多大影响。MOT算法中起决定作用的是检测，鉴别特征和数据关联。

经典多目标跟踪算法介绍

多假设跟踪(MHT)

多假设跟踪本质上是卡尔曼滤波方法在多目标跟踪任务上的拓展。定义$k$时刻之前的检测响应为$z^k$, 历史总的检测响应为$Z^k$, 多假设跟踪的目标是求解已有轨迹和当前检测之间关联的条件概率模型。把似然关联假设$\Theta_k$划分为当前关联假设$\theta_k$和$k-1$时刻的关联假设$\Theta_{k-1}$, 那么依贝叶斯推理可以得到

$\begin{align} P\{\Theta_k|Z^k\} &= P\{\theta_k, \Theta_{k-1}|z^k, Z^{k-1}\} \\ &= \frac{1}{c}p[Z^k|\theta_k,\Theta_{k-1}]P\{\theta_k|\Theta_{k-1}, Z^{k-1}\}P\{\Theta_{k-1}|Z^{k-1}\} \end{align}$

后验概率通过贝叶斯公式转换为先验概率。最下面一行等式右边第3项是$k-1$时刻的后验概率，第2项是$k$时刻之前的检测响应和对应轨迹的条件下计算当前时刻关联假设的概率，第1项是在获得当前项和历史关联假设前提下出现当前检测响应的概率。$c$是推导过程中的分母，常数，用于保证概率范围。该公式逐帧计算是迭代过程，每一帧需要计算第1,2两项。

MHT采用两个概率模型建模第1,2两项

用均匀分布和高斯分布对关联对应的检测观察建模.

用泊松分布对当前假设的似然概率建模

前者表示，当检测响应来自轨迹$T$时，它应符合$T$在当前时刻的高斯分布，否则认为是一个均匀分布的噪声，类似于卡尔曼滤波跟踪。后者表示，在误检和新对象出现概率确定的情况下，出现当前关联的可能性可以通过泊松分布和二项分布的乘积表示。在以上假设下，关联假设的后验分布是历史累计概率密度的连乘，转化为对数形式，可以看出总体后验概率的对数是每一步观察似然和关联假设似然的求和。因此，选择最佳的关联假设，转化为观察似然和关联假设似然累计求和的最大化。在具体算法中， I.J.Cox等人提出一种基于假设树的优化算法，如下图

MHT

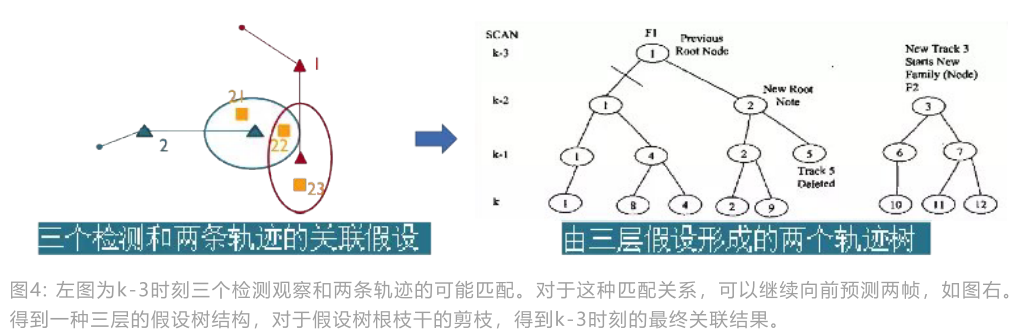
可以发现其实MHT有局部遍历的思想，并且利用到了之后的信息，属于离线方式。

任何时刻都可能存在多种假设关联，因此到k时刻的假设构成了一种组合假设树的层次关系。例如图4左边表示的是2个轨迹和3个观测之间可能形成的关联假设，可能存在的假设有{观测 23=>轨迹1，观测22=>轨迹2, 观测21=>新轨迹}或者{观测22=>轨迹1，观测21=>轨迹 2, 观测23=>新轨迹}，因此产生2个假设分支。图4右侧是从这2个关联假设出发的三层假设树关系，可以看出随着假设层数的增多，关联假设出现组合爆炸的可能。因此进行必要的剪枝减少假设空间的数目是必须的步骤。那么如何选择最佳的关联呢？I.J.Cox采用了2个步骤来实现。首先，限制假设树的层数为3层。其次，是对每个分支的叶节点概率对数进行求和，最大的分支进行保留，即选择边缘概率最大的那个分支假设作为最后选择的关联。可以把这种选择方法简单的表示为：

$S(k-3) = \frac{1}{|H(k)|}\sum_{\theta^k\in H(k)}\log([Z^k|\theta_k,\Theta_{k-1}])+\log(P\{\theta_k|\Theta_{k-1}, Z^{k-1}\})$

其中$H(k)$是所有可能的假设集合，所以上式是从多个假设中筛选置信度最高的假设作为跟踪结果。

这种基于似然概率对数累加的方法虽然方便迅速，但是存在一个主要的限制，即假定观测关联符合高斯模型，并且在每一步选择关联假设之后，需要利用Kalman滤波更新轨迹状态。通过对MHT基本公式(1)的扩展，可以建立不同的概率模型描述这种多假设关联的全局概率，例如Kim等人在ICCV2015和ECCV2018通过归一化的最小均方差优化算法引入表观模型来扩展MHT算法，取得不错的多行人跟踪结果.

基于检测置信度的粒子滤波算法

该算法可分为两个步骤：

利用贪心算法，将每一帧检测结果分配给已有的轨迹结果
利用匹配结果，计算每个对象的粒子权重，作为粒子滤波框架中的观测似然概率。

粒子滤波框架如下图所示：

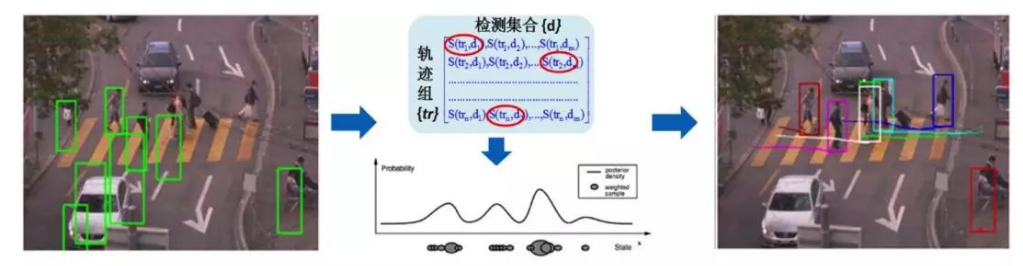
分别表示检测响应，构建相似度矩阵，计算每个粒子群权重，贪心算法或者匹配，重新计算当前目标位置。

具体步骤如下：

计算历史轨迹与当前检测响应的相似度
$S(tr, d) = g(tr, d)[c_{tr}(d) + \alpha \sum_{p\in tr}^Np_N(d-p)]$
tr表示轨迹， d表示检测。所以相似度包含3方面：$c_{tr}(d)$表示在线学习的分类器结果；粒子与检测的匹配度采用高斯密度函数度量，$p\in tr$表示轨迹对应的粒子群， $p_N(d-p)$表示高斯相似度；与检测尺寸大小相关的阈值函数$g(tr,d)$表示轨迹与轨迹尺度上的契合程度， $\alpha$用于控制粒子群的松紧度。

计算出匹配亲和度矩阵之后，可以采用二部图匹配的Hungarian算法计算匹配结果。不过作者采用了近似的贪心匹配算法，即首先找到亲和度最大的那个匹配，然后删除这个亲和度，寻找下一个匹配，依次类推。贪心匹配算法复杂度是线性，大部分情况下，也能得到最优匹配结果。
采用粒子滤波框架，更新每条轨迹的粒子权重。
$w(tr, p) = \beta\cdot I(tr)\cdot p_N(p-d^*) + \gamma \cdot d_c(p)\cdot P_o(tr) + \eta\cdot c_{tr}(p)$
$I(tr)$是示性函数,表示轨迹在该帧中是否关联成功，成功的话，则计算粒子在关联检测为中心的高斯概率；$d_c(p)$是粒子的检测可信度， $p_o(tr)$是权重函数
$p_o(tr)=\begin{cases} 1, \quad\quad\quad&\text{if} \quad\quad I(tr)=1,\\ \max_{tr':I(tr')=1}p_N(tr-tr') \quad\quad &\text{elif}\quad \exists ~~I(tr')=1 \\ 0 &\text{otherwise} \end{cases}$
表示当轨迹匹配的时候权重为1，否则去附近成功匹配轨迹的最大高斯密度，若周围没有成功匹配，则权重为0.

结合检测可信度的粒子滤波算法对轨迹的初始化采用了感兴趣区域的简单启发式策略。即，进入图像区域边框时，初始化对象；当连续多帧没有关联到检测时终止跟踪。在一些典型数据集上，基于检测可信度的粒子滤波算法可以得到不错的结果。

基于最小代价流的跟踪算法

该算法是一种确定性优化离线方法，其目标函数是从已知的检测结合中找出最优的轨迹集合

$T^* =arg\max_T P(T|D) = arg\max_T\prod_iP(d_i|T)P(T)$

表示成对数形式

$T^* = arg\min_T\sum_{T_k\in T}(-\log P(T_k) + \sum_i-\log P(d_i|T_k))$

第一项刻画轨迹存在的概率，第二项表示该轨迹存在前提下对应该检测的概率。

每条轨迹表示成链接的检测后，其能量可以表示为

$f^* = arg\min\sum_i C_{si}f_{si} + \sum_i C_if_i+\sum_{i,j}C_{ij}f_{ij} + \sum_iC_{it}f_{it}$

其中$f_{si}, f_i, f_{ij}, f_{it}$均为示性变量分别表示是否是起点，是否在轨迹上，是否后续连接$j$节点，是否是终点。由于MOT任务中一一对应假设，所以节点$i$前后只存在一个连接，$f_{si} + \sum_j f_{ji} = f_i = \sum_{j}f_{ij}+f_{it}=1 ~\text{or}~0$

网络流优化问题满足最小代价流模型：

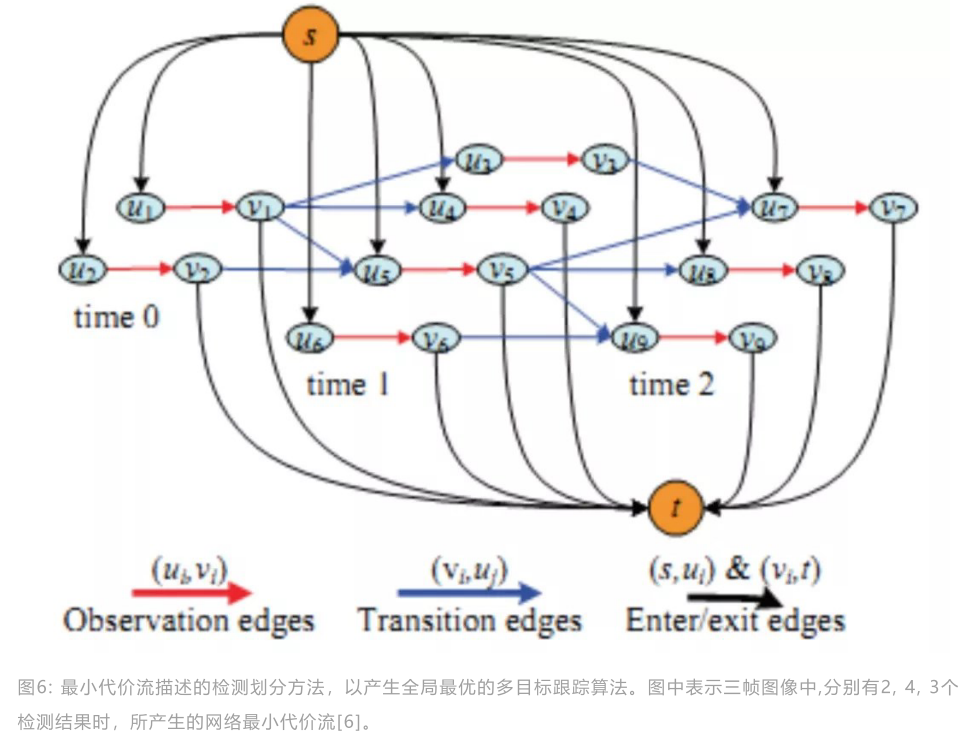
min-cost-flow

边的代价函数计算规则：

$\begin{align} C_{si} &= -\log P_{enter}(x_i)\\ C_{it} &= -\log P_{exit}(x_i)\\ C_{ij} &= -\log P_{link}(x_j|x_i)\\ C_i &= \log(\beta_i/(1-\beta_i)) \end{align}$

迹数目通过迭代比较的方法确定. 注意到检测节点代价Ci 的值是一个负数，所以轨迹对应的网络流代价也可能小于0。因此，通过遍历不同轨迹数目，可以确定一个全局代价最小的解。这种方式效率较低。

基于马尔科夫决策(MDP)的跟踪算法

MDP是一种在线确定性推导方法。

该方法把目标跟踪看作是状态转移过程。马尔科夫决策过程包含四个元素$(S, A, R, T)$, 分别表示状态集合、动作集合、状态转移集合和奖励函数集合。一个目标的跟踪过程包括如下决策过程：

从Active状态转移到Tracked状态或者Inactivate状态，表示新出现的检测是否确实是轨迹。
从Tracked状态转移到Tracked状态或者Lost状态，表示跟踪继续或者终止。
从lost状态转移到Lost状态或者Inactivate状态或者Tracked状态，即判断丢失的对象被重新跟踪或者终止或者继续处于跟丢状态。

MDP

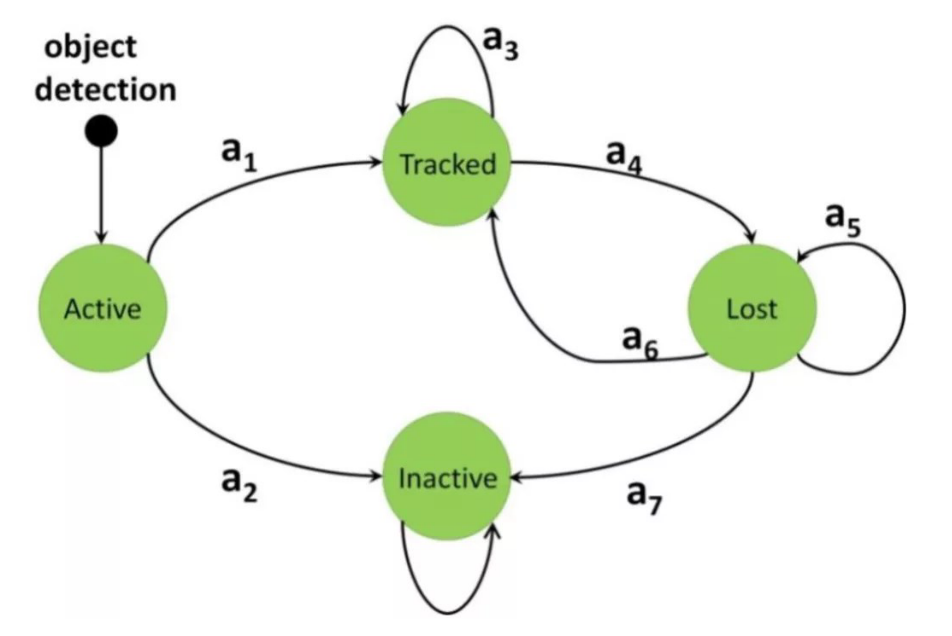
三种决策过程分别对应着不同的奖励函数。

$R_{activate}(s, a) = y(a)(w_{activate}^T\phi_{activate}(s)+b_{activate})$ $y(a) = \begin{cases} 1, &\text{if} \quad a=a_1\\ -1, &\text{else} \quad a=a_2 \end{cases}$
这一步主要用来判断检测是否是目标。论文中使用离线训练的SVM实现该过程。检测样本的特征包括$(x,y, w, h, d_s)$
$R_{Tracked}(s, a)=\begin{cases} y(a) &\text{if}\quad e_{medFB}<e_0, \text{and} \quad o_{mean} > o_0\\ -y(a) &\text(else) \end{cases}$
$a=a_4$时， $y(a)=1$，否则$y(a_3)=-1$, $e_{medFB}, o_{mean}$分别表示光流中心偏差和平均重合度， $e_0, o_0$分别表示阈值。
$R_{Lost}(s, a) = y(a)(\max_{k=1}^M(w^T\phi(t, d_k)+b))$
计算$M$个匹配模板与检测的匹配程度，判断是否存在使得上述奖励最大且非负的匹配，当存在是选择$a=a_6$，不存在是判断是否连续丢失次数超出阈值$T_{Lost}=50$，超出则$a=a_7$, 否则$a=a_6$.

这部分可能理解起来存在些困难。其实需要弄明白的是，强化学习中首先根据当前的状态计算能量，然后根据能量来选择动作使得奖励最大。比如第一种奖励，首先计算等式右边第二项，根据其值大小来选择$a$是执行$a_1$还是$a_2$从而使$R_{active}$最大。

基于局部流特征的近似在线多目标跟踪（NOMT）

这种方法称为近似在线多目标跟踪的原因在于跟踪$k$时刻目标时仅利用了之前的信息，但是该时刻依然允许对之前时刻跟踪结果进行修改。

其主要思想：对于当前帧$t$, 回看$\tau$帧，在这个时间间隔内构造若干轨迹片段, 利用这些轨迹片段跟之前的轨迹进行关联跟踪。轨迹片段包含了最新的$\tau$帧信息，因此如果该时间段内发生了匹配错误，依然允许进行修改。其基本思想如下图所示

NOMT

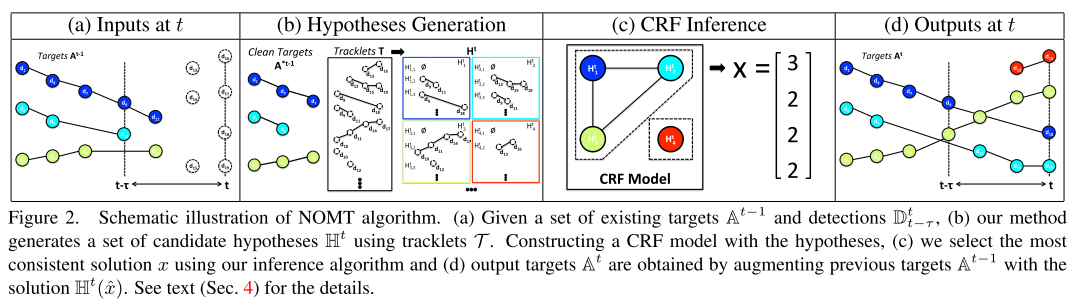
该部分的具体内容，请参考博客园

Conclusion

以上讨论了一些经典的传统多目标跟踪方法，这些方法虽然目前相对于基于深度的方法性能稍弱，但是作为基本的baseline，思想值得借鉴。