阅读笔记-Online Multi-Target Tracking Using Recurrent Neural Networks

Abstract

本文第一次提出利用深度网络端到端的实现多目标跟踪。

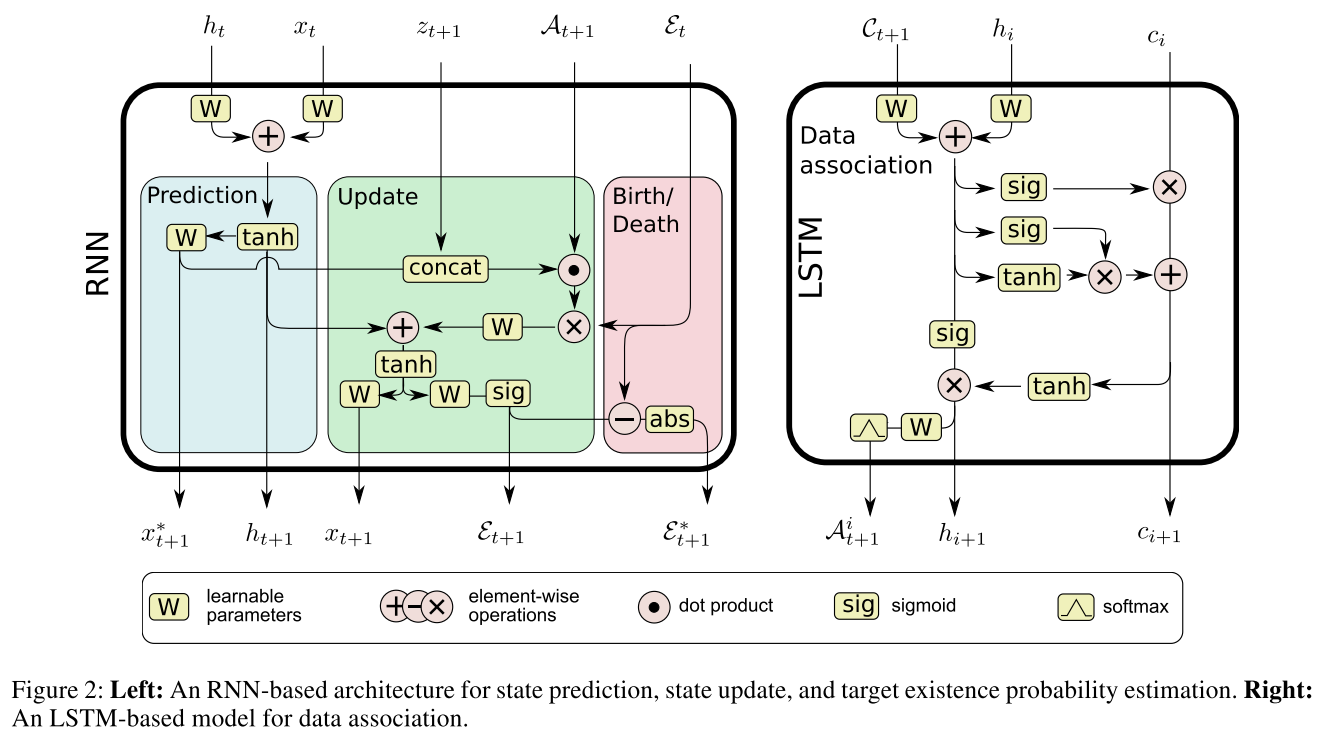
architecture

真实环境中处理多目标跟踪任务具有一些难点。首先轨迹的个数不定，轨迹的起点和重点不定；其次轨迹中目标的状态是连续变量，比如位置，尺寸，置信度等，最后一般解决多目标跟踪任务最终转化为组合优化问题，而组合优化问题是离散空间求解问题。

这篇文章和之前的两篇笔记一样，都是利用网络去解决数据关联问题。

项目地址： https://bitbucket.org/amilan/rnntracking

Introduction

为什么不能直接将用于NLP的RNN用在MOT任务上？

NLP中每次预测的是一个词或者字符，但是MOT任务中每次预测需要预测多个目标，即状态空间是多维的。
NLP中预测的单词或者词汇可以用one-hot等方法转化为离散变量，但是MOT任务中目标状态既包括离散值又包括连续值。比如连续的位置，大小等，而数据关联则是离散空间内的求解。
每一个时刻目标个数不同就导致输出个数随着时间而变化。

Recurrent Neural Networks

RNN主要用于处理序列化数据，每个时刻的输入包含当前时刻的数据以及前一时刻的状态。一般而言，每一时刻的处理可以使用多层网络实现，在$t$时刻的多层隐状态可以使用$h_t^l, l=0, …, L$表示， $h_t^0$表示当前时刻的输入， $h_t^L$表示最终用于生成输出值$y_t$的embedding 特征。每一层形式化表示为$h_t^l = \tanh W^l(h_t^{l-1}, h_{t-1}^l)$ .

RNN在运动估计、状态更新方面效果较好，但是其并不能很好的处理数据关联这种组合任务。因此使用LSTM单元处理这类问题。 LSTM单元相对于RNN单元多出了一个记忆状态量$c$, 然后经过多个门函数对状态信息进行遗忘，更新和输出等，其形式化表示为$h_t^l = o\odot \tanh(c_t^l), c_t^l = f\odot c_{t-1}^l + i\odot g$, $\odot$表示元素乘法。

$i, o, f = \sigma[W^l(h_t^{l-1}, h_{t-1}^l)]$

Bayesian Filtering

假设真实状态$x$, 观测量$z$, 利用马尔科夫假设，当前时刻的状态分布计算为

$p(z_t|z_{1:t}) \propto p(z_t|x_t)\int p(x_t|x_{t-1})p(x_{t-1}|z_{1:t-1})dx_{t-1}$

$p(z_t|x_t), p(x_t|x_{t-1}) $分别表示观测概率和转移概率。一般分为预测和状态更新两步。典型的模型有kalman滤波和粒子滤波。

处理多目标任务时还会遇到两个额外的挑战：

状态更新前需要先利用数据关联确定目标和检测的对应关系。
应该有机制能够处理新的轨迹以及移除终止的轨迹。

Approach

Notations

$x_t\in R^{N\cdot D}$ 特定时刻所有目标的状态，本文$D=4$，包含$(x, y, w, h)$, $N$是目标个数。

$x_t^i$ 表示第$i$个目标的状态

$z_t\in R^{M\cdot D}$ 表示当前时刻检测的状态。

$A\in [0, 1]^{N \times (M+1)}$ 关联矩阵， $\forall i: \sum_j A_{ij}=1$, $M+1$考虑了一些目标当前出现漏检的情形。

$\varepsilon \in [0, 1]^N$ 表示目标在当前帧依然存在的概率。

$\sim$ 该符号表示对应变量的groundtruth

MTT with RNNs

方法将MOT任务分解成两部分。一部分包含状态预测、更新和track管理，另一部分包含数据关联。

好处：

每个模块可以分开调试
模块化之后可以简单的通过替换不同模块进行测试
分成模块单独训练可以加快收敛

Target Motion

如Fig2的左图所示， RNN模块的输入包含上一时刻的隐变量$h_t$, 状态量$x_t$, 当前时刻的观测量$z_t$, 关联矩阵$A_{t+1}$, 以前上一时刻目标存在与否的概率向量$\varepsilon_t$. 输出五个量：隐变量$h_{t+1}$, 当前预测状态和更新后状态$x_{t+1}^, x_{t+1}$, 当前每条轨迹依然存在的概率$\varepsilon_{t+1}$以及轨迹存活概率的绝对变化差值$\varepsilon_{t+1}^$

三个模块分别对应：

predict：学习复杂的动态模型用于预测目标状态
Update：利用当前观测去更新目标状态
Birth/Death: 根据目标状态来判别当前时刻检测是目标轨迹的起点还是终点

值得注意的是，这里的$x_{t+1}^, z_{t+1}$*concat时利用的是关联矩阵$A_{t+1}$的信息

Loss

$\mathcal{L}(x^*, x, \varepsilon, \tilde{x}, \tilde{\varepsilon}) = \frac{\lambda}{ND}\sum\Vert x^* - \tilde{x}\Vert^2 + \frac{k}{ND}\Vert x-\tilde{x}\Vert^2 + v\mathcal{L}_{\varepsilon}+\xi\varepsilon^*$

等式右边三项分别表示预测误差，更新误差以及birth/death+reg误差。

$\mathcal{L}_{\varepsilon}(\varepsilon, \tilde{\varepsilon}) = \tilde{\varepsilon}\log \varepsilon + (1-\tilde{\varepsilon})\log (1-\varepsilon)$

二值交叉熵损失。

由于$\tilde{\varepsilon}$真实值是一个相对于时间的矩形窗函数，如果单独采用二值交叉熵损失，特别容易导致漏检引起轨迹终止的问题，于是加了一个正则化项用于平滑损失。如下如所示：

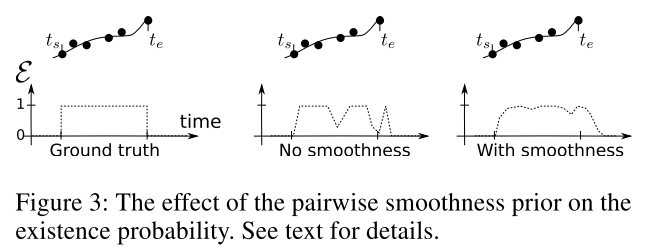
smoothness

最左边是真实值，中间是没有正则项的结果，最右是正则化项辅助下的记过，黑色点和线表示轨迹，中间点没有均匀分布表示出现漏检，而中间图中漏检对应的地方其$\varepsilon$都很低，表示轨迹结束。

Data Association with LSTMs

LSTM的输入是$C|{ij} = \Vert x^i - z^j\Vert_2$矩阵，即欧氏距离矩阵，输出是匹配概率矩阵$A$, $A$的每一行执行softmax归一化，保证每一个轨迹只关联一个检测。

Loss

负对数似然损失

$\mathcal{L}(A^i, \tilde{a}) = -\log (A_{i\tilde{a}})$

$\tilde{a}$是正确的关联关系。

Training Data

由于视频数据标注代价太大，文章使用了大规模的合成数据。具体而言，首先从已知的轨迹中构建一个运动模型（估计轨迹起点位置以及平均速度的均值和方差）然后对于每一个训练样本就可以通过采样的方式生成$N$个训练样本。

Network size

RNN单元只有一层300个隐节点， LSTM单元两层500个隐节点。

Data

RNN训练数据： $100K$ 长度为20帧的长序列。 mini-batches的大小为每个10，图像中目标数据归一化为[-0.5, 0.5]。

Experiments

Simulated data

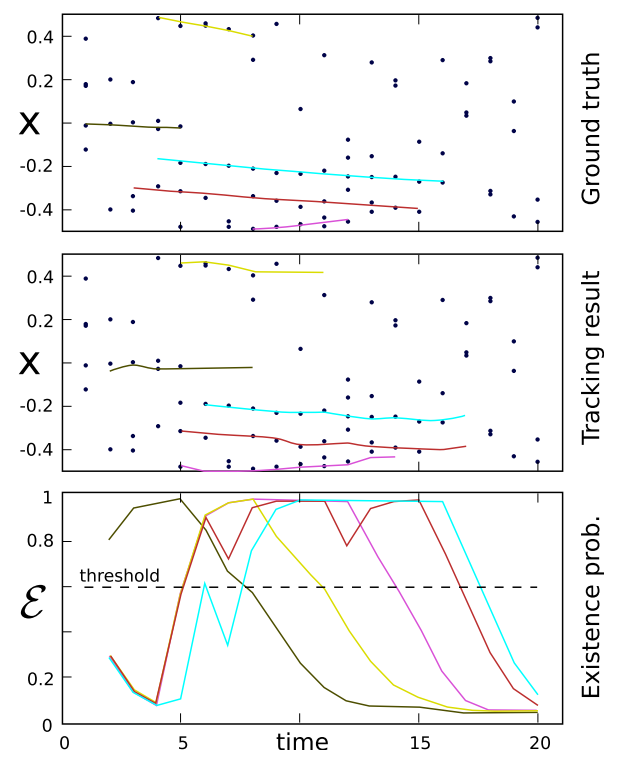
simulated data

分布的点表示每一时刻目标的位置，groundtruth或者detections，没有形成轨迹的点是一些噪声点。最先面是用来判断轨迹终止的概率，可以发现在合成数据上效果还是不错的。

MOT15

MOT15 training

MOT15 test

实验可以发现这篇文章主要还是在RNN做数据关联方面一个全新的尝试，其效果并不理想，尤其是在test集上，这可能是因为训练数据集太少。另外在训练集上我们也发现RNN_HA的效果比RNN_LSTM效果要好，这说明LSTM实现data association的效果目前还比不了匈牙利算法。

Conclusion

加上前面的两篇笔记，总共三篇文章都是在尝试用深度网络直接实现数据关联。总的来说Milan大神的这篇文章出现的最早，但由于技术的原因吧性能不好，所以后续研究不多。目前随着数据量的增大以及检测精度的增加，基于CNN做数据关联的工作开始逐渐崭露头角。

我觉得用深度网络实现数据关联一定会是一个发展趋势，只有数据关联部分使用网络实现了，才能真正意义上说是用深度学习解决多目标跟踪任务。