深度学习-检测器的评价指标 mAP [代码]

本文翻译自Measuring Object Detection models - mAP - What is Mean Average Precision?

对于大多数利用机器学习方法求解的问题来说一般都会存在多个可用模型。 每一个模型都有自己的特点，从而在不同的因素作用下，其表现性能也会出现差异。

模型的性能一般通过其在某个数据集上的表现来评价， 一般这个数据集是对应于训练集的“验证集”或者“测试集”。 性能的定量评价可以有多重指标，比如 acc， pre和recall等。具体选择哪一种指标取决于具体应用和场景。而对于同一种应用，找到一个能够公正合理的比较不同模型的指标则非常重要。

这篇文章我们将会讲一讲目标检测问题中最常见的评价指标 mAP, (The Mean Average Precision)

大多数任务中，评价指标都是通俗易懂且容易计算的，比如二分类任务中的正确度(precision)和召回率(recall)都是直观且容易计算的。

但目标检测问题却是个相当与众不同而且比较有意思的任务。

在目标检测任务中，假设检测器从一幅含猫的图像中检测到了猫，但如果没有定位到猫的位置，那结果没有任何意义。

所以在目标检测任务中需要预测图像中目标是否出现(occurence)的同时确定目标位置， 那么该如何度量这种指标呢？

首先，我们需要先定义一下什么事目标检测问题。

目标检测

目标检测是指：

“ 给定一幅图像，从图像中找到目标，确定目标的位置并分类目标”

由于目标检测模型一般指定了学习的类别， 因此检测模型只需要定位于区分这些指定的类别。另外一般使用矩形框bounding box来定位目标。

所以，目标检测任务包含定位和分类两个子问题。

下面要介绍的mAP指标特别适合那些定位不同类目标的算法，所以mAP可以用来评估下图中的定位模型，目标检测模型和目标分割模型。

---

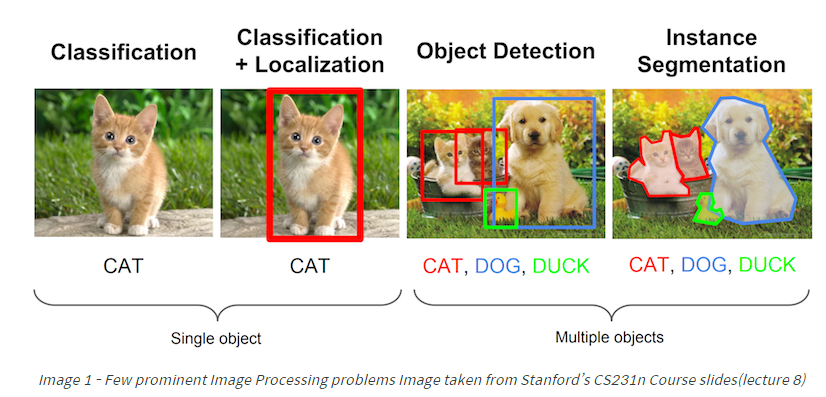
评价目标检测模型

为什么选择 mAP指标？

在目标检测任务中， 每张图像都可能包含不同类别中的不同目标。而这些目标的定位和分类都需要评估。 因此图像分类任务中的标准评价指标不能直接应用到目标检测任务中。 于是mAP进入了视野。

关于ground truth

无论是什么算法，评估算法性能都是比较算法的输出和样本的真是标签。对于目标检测任务，ground truth 数据包括图像、目标的类别以及目标在图像中真是的标定框。

如下图所示， 图像，类别和标定框。当然，一般数据集的ground truth数据都是给定一幅图像以及对应的一串包含类别和标定框信息的文本内容。我们将文本内容表现在图像上从而更直观。

下面我们重点来介绍下mAP是如何计算的get our hands dirty, 首先我们假设已经获得某个检测器在验证集上的检测结果，希望评价这个检测器的性能。

计算mAP

检测器一般会输出大量的预测结果，但是其中大部分预测的置信度都比较低，所以在评估时只考虑那些置信度超出指定阈值的预测结果。

将验证集的某张图像输入检测器中，经过与预测结果置信度阈值筛选后的预测结果就是检测器的最终输出。

比如下图：

我们可以很直观的说这些检测是正确的，那么如何该如何量化的表示检测结果呢？

首先我们需要度量这些检测结果的正确性。一般使用 IOU （Intersection over Union) 来预测boundingbox的正确性。 IoU是一个非常简单的视觉量。

下面详细的介绍了IoU的计算过程。

IOU

IoU是指预测的bounding box与真实的bounding box的交集面积与并集面积的壁纸。也被称为Iaccard Index, 最早是由Paul Jaccard在19世纪初提出。

为了计算交并值，需要将预测框和真实框重叠在一起。对于每一类而言，检测框和真实框重叠的部分称为交集，而检测框和真实框覆盖的总区域称为并集。如下图中关于马 这类的交并比

IoU计算的图形化表示如下

识别正确的检测并计算正确率和召回率

和所有的机器学习算法一样，为了计算正确率和召回率，首先需要区分True Positives， False Positives, True Negatives 和 False Negatives.

我们使用IoU来筛选True和FALSE Positives。大多数情况下IoU的阈值为$0.5$, 也就是说当一个检测与同类别的某个ground truth 框的IoU大于 0.5时认为这个检测框属于True positive， 否则被认为是False Positive。 COCO数据集评测时建议通过交叉验证来获得IoU的阈值，这里为了简单，我们采取PASCAL VOC的度量标准， 即将阈值固定为0.5

计算召回率时，需要计数negative的个数，按照分类问题中的定义，图像中所有没预测到目标的部分都可以认为是负样本，但这种假设导致true negative没有任何实际意义，（即true negative可能就只是背景）。所以这里只计算“False” Negatives， 即没有被检测到的目标的个数。

另外一个需要考虑的因素是模型给出的每个检测的置信度。 通过置信度阈值的调整，划分为正样本positives的检测肯定不同。基本上所有的预测，（与类别无关），如果置信度大于阈值就是positive box，小于阈值就是negative box。

对于每一张图像，其groundtruth数据能够得知图像中每一类目标的真实个数。

通过阈值筛选出所有的positive detections之后，可以计算positive detections与ground truth之间的IoU。 然后利用这些数值与预先设定的IoU阈值可以找出每一张图像中correct detections的个数。从而计算出每一类的正确率precision

$$\frac{TP}{TP+FP}=\frac{TP}{P}$$

获得正确检测(True Positives)的个数，以及错误检测(False Positive)的个数后, 其召回率，即所有的ground truth中检测到的比率可以如下计算

$$rec = \frac{TP}{FN+TP} = \frac{TP}{|G_t|}$$

计算mAP

• 使用PASCAL VOC的评价标准。

  mAP在不同的领域有着不同的定义。 该度量广泛应用于信息检索和目标检测领域。 而在这两个领域中mAP的计算方式也不同。 这里讲的是目标检测领域内的mAP计算方式。

  目标检测领域内mAP是PASCAL VOC Challenge首先形式化表述的。 详见具体论文paper

  我们本节计算mAP中使用的pre和rec计算方式和前面一节方法相同。

  正如前文所说，计算pre和rec时，有两个很重要的阈值， 即置信度阈值和IoU阈值。

  IoU是一种简单的几何度量，可以很容易的标准化处理，比如PASCAL VOC中全部基于IoU=0.5条件下计算mAP， COCO则更进一步在不同的IoU阈值$5\% \sim 95\%$下计算mAP。但置信度阈值却随着模型不同变化很大。在一个模型中$50\%$置信度很可能等价于其他模型中$80\%$的置信度， 这就会导致pre-rec曲线形状差别很大。于是PASCAL VOC的组织者提出了一种解决办法。

  文章中建议计算一种AP的度量。

  > For a given task and class, the precision/recall curve is computed from a method’s ranked output. Recall is defined as the proportion of all positive examples ranked above a given rank. Precision is the proportion of all examples above that rank which are from the positive class. The AP summarises the shape of the precision/recall curve, and is defined as the mean precision at a set of eleven equally spaced recall levels [0,0.1,...,1]:
  >

  也就是说将置信度阈值划分为11个不同的取值， 使得每一个阈值确定的recall分别为$0, 0.1, 0.2, …, 0.9, 1.0$

  于是 AP定义为这11个rec对应的pre的平均值。 而mAP则是所有类别的AP的均值。

个人分析：召回率的计算是TP与所有ground truth的比值，ground truth的个数是一直的，那么就可以通过选择不同个数的TP来保证recall在特定的数值上。因此具体计算时可以将detections按照置信度降序排列，然后已从从前往后选择不同个数的TP获得对应的recall，同时计算对应的pre。

在计算precision时采用的是一种插值方法：

> The precision at each recall level r is interpolated by taking the maximum precision measured for a method for which the corresponding recall exceeds r
>

即对于某个recall值r， precision值取所有recall>r值中的最大值， 保证了p-r曲线单调不增

$$p_{interp}(r) = max_{\hat{r}\gt r} p(\hat{r})$$

关于计算recall对应的precision时可能有点难理解，下面我们通过示例来解释一下example

假设检测器对下面7张图片的检测结果为（绿色标识ground truth， 红色表示检测结果， 数字表示置信度）

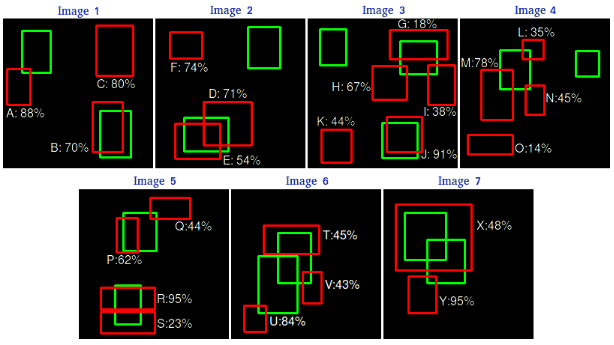
那么如果将IoU阈值设为$0.3$,就可以判断每个检测是否是真正的positive， 在计算IoU进行配对时，每个ground truth最多只能对应一个检测，所以当多个检测与同一个ground truth IoU都大于阈值时，选择最大IoU的那个检测，其余的都不能分配给这个ground truth，再与其他的ground truth匹配。

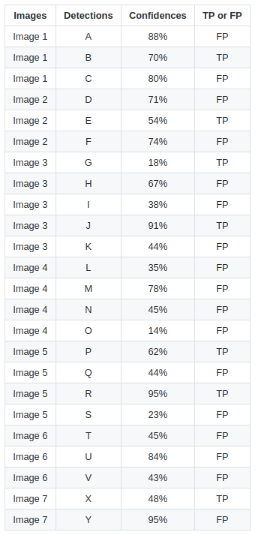
然后对所有的检测按照置信度降序排列，然后通过逐渐增多认为是positive的检测的个数，可以得到每个阈值下对应的rec和pre

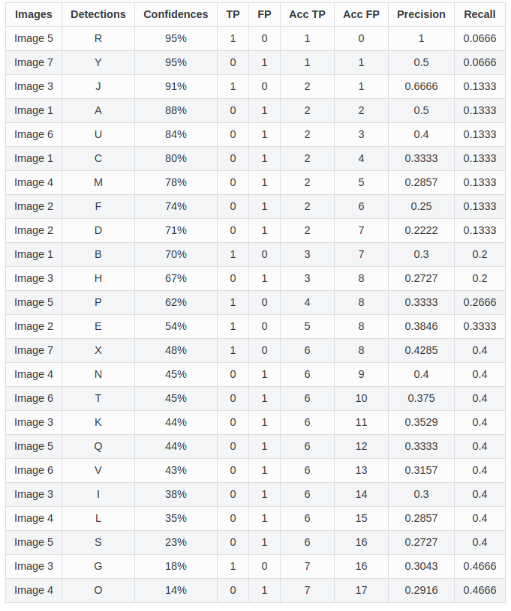
Acc TP， Acc FP 表示将每个检测的置信度设为阈值时的累积TP和FP。 由累积的TP和FP可以计算每个阈值下的pre和rec

$$pre=\frac{tp_a}{ tp_a + fp_a}\\ rec = \frac{tp_a}{N_d}$$

那么将每一对(rec, pre)绘制在平面上得到：

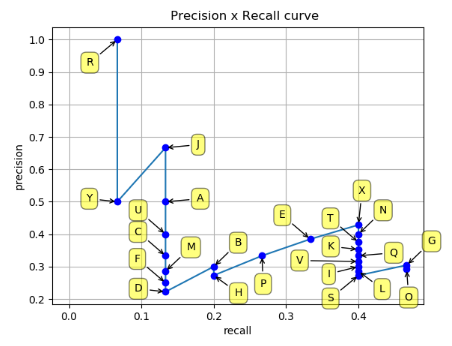
可以返现曲线并不是单调的，而且一个rec可能对应着多个pre，这时候采用11点插值的做法是，将rec均匀采样为11个点，每一个点可能并不恰好对应于上图中的节点，比如rec没有等于0.1的点，这时候就需要插值得到对应的点的坐标(rec, pre). AP是pre-rec曲线的AUC（area Under Curve）

按照上文所说，每一个选中的rec对应的pre是大于该rec的所有点中最大的pre值。于是得到下图. 比如 rec=0.0时肯定找不到对应的点，这时候找所有rec>0.0时的点对应的最大pre值作为0.0对应的pre，同理像是rec=0.2， rec=0.3时找到的对应pre都与rec=0.4时相同。

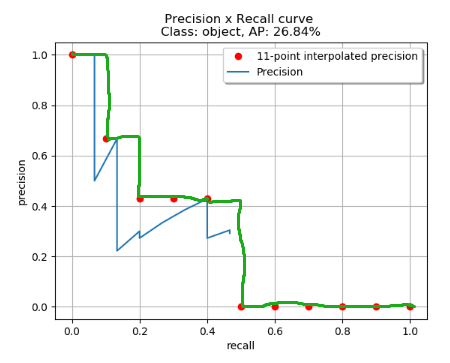
那么阶梯状连接所有的插值点，计算线下面积就是VOC标准下的mAP值。

$$AP = \frac{1}{11}(1 +0.6666+0.4285+0.4285+0.4285+0+0+0+0+0) = 26.84\%$$

而采用COCO标准的计算方法不同

COCO计算所有点对应的rec和pre， 而不是对rec进行均匀采样。其一般操作如下图所示, rec从1逐步下降到0， pre选择遍历过程中出现的最大值。

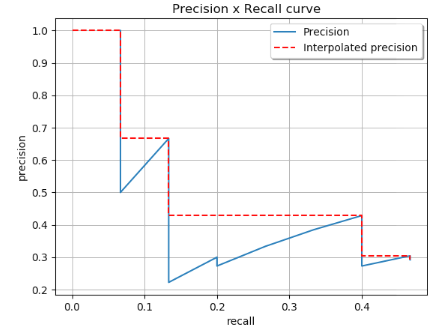
所以COCO标准下，同样的检测结果， mAP计算为

$$A1 = (0.0666-0)*1=0.0666; \quad A2 = (0.13333-0.0666) * 0.6666 - 0.0445\\ A3 = (0.4-0.1333) * 0.4285 = 0.1143; \quad A4 = (0.4666-0.4)*0.3043 = 0.0203\\ AP = 24.46\%$$

发现两个标准下还是存在不同的，其实对比两张曲线图可以发现线下面积的不同。首先VOC是是rec进行了均匀采样，而COCO没有。其次COCO对原始曲线的包络更紧致，也更准确。

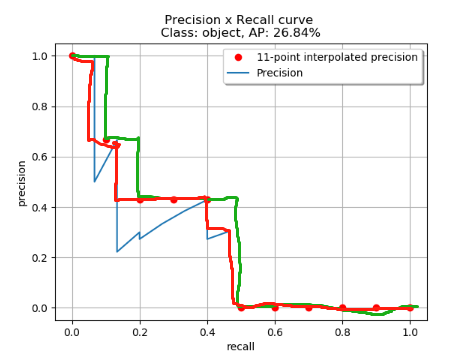
一些比较mAP值时需要注意的地方

• mAP是在相同数据集上计算得到的。
• 虽然很难绝对的量化模型的输出，但mAP是一个相对来说很好的度量，许多常用的数据集都是用mAP对比方法。
• 对于特定类别的AP值可能非常高也可能非常低，这取决于特定数据和类别。所以mAP是一种这种的量。但在分析的时候应该分析一下每一类的AP值，从而知道模型对于那些数据类别表现较好并分析原因。

mAP的开源代码

• 计算每多一个detection作为positive下， 对应的pre和rec指标

  sorted_ind 	= np.argsort(-confidence)  # 置信度降序排列下的索引
  BB 		   	= BB[sorted_ind, :]  # 所有的检测框按照置信度降序排列， 检测框来源于多张图像
  image_ids 	= [image_ids[x] for x in sorted_ind] # 每个检测对应的图像
  nd 			= len(sorted_ind)   # 检测结果的个数
  tp 			= np.zeros(nd)
  fp 			= np.zeros(nd)  # 每个检测的标志位， 1表示是fp， 0表示不是， tp与fp类似
  for d in range(nd):  # 遍历每一个检测，判断其是否是positive
      R 		= class_recs[image_ids[d]]  # 对应图像中的标注信息
      bb 		= BB[d, :].astype(float)  # bounding box的4个值
      ovmax 	= -np.inf   # 与ground truth的最大overlap
      BBGT 	= R['bbox'].astype(float)  # 当前图像对应的所有ground truth boxes
      
      if BBGT.size > 0:  # 存在gt box， 则计算检测与gt box的iou配对
          xmin = np.maximum(BBGT[:, 0], bb[0])
          xmax = np.minimum(BBGT[:, 2], bb[2])
          ymin = np.maximum(BBGT[:, 1], bb[1])
          ymax = np.minimum(BBGT[:, 2], bb[2])
          w = np.maximum(xmax - xmin + 1, 0.)
          h = np.maximum(ymax - ymin + 1, 0,)
          inters = w * h  	# intersection
          unions = (bb[2] - bb[0] + 1.) * (bb[3] - bb[1] + 1.) +
          		 (BBGT[:, 2] - BBGT[:, 0] + 1.) *(BBGT[:, 3] - BBGT[:, 1] + 1.) -
              	 inters   # union
                  
          ious    = inters / unions
          ovrmax 	= np.max(ious)  # 与gt boxes存在的最大的iou
          jmax 	= np.argmax(ious)  # 最大iou的gt box的索引
      if ovmax > ovthresh: 		# 大于IoU阈值则认为是匹配成功的
          if not R['diffcult'][jmax]:  # 非diffcult的样本参与评估
              if not R['det'][jmax]:   # 如果该ground truth没有被分配过检测，则分配
                  tp[d] = 1
                  R['det'][jmax] = 1  # 用来保证每个gt只分配最近的检测
              else:
                  fp[d] = 1   # 该检测没有分配成功
      else:
          fp[d] = 1
  fp 		= np.cumsum(fp)  # 累积fp值 fp_a
  tp 		= np.cumsum(tp)  # 累积tp值 tp_a
  rec 	= tp/ float(npos)  # npos表示所有ground truth的个数
  pre 	= tp/np.maximum(tp + fp, np.finfo(np.float64).eps)  # 防止分母为0

  我认为这部分计算其实是存在问题的

  举个例子， 现在有两个gt分别为gt1, gt2, 检测器检测出两个响应d1, d2, 其置信度分别为0.7和0.6，

  计算d1, d2与gt1， gt2的iou矩阵如下

  | - | gt1 | gt2 |
  | —— | —— | —— |
  | d1 | 0.8 | 0.6 |
  | d2 | 0.7 | 0.68 |

  那么按照上面提供的代码计算得到的值

  $$TP = [1, 0] ;\quad \quad FP = [0, 1]$$

  但直观上来看， d2既然不能分配给gt1了，那为什么就不能分配给gt2了呢？而直接就认为d2是false positive了呢？

  所以我觉得这部分计算TP， FP的过程还是MOT中的CLEAR指标中方法更加合适，采用贪婪法或者匈牙利算法对检测和gt进行匹配， 匹配之后再进行统计TP和FP。

• 由pre， rec计算最终的mAP

def voc_ap(rec, pre, use_07_metric=True):
    """Compute VOC AP given precision and recall. If use_07_metric is true, uses the VOC 07 11-point method (default: False)"""
    if use_07_metric:  # 07年方法，即11点插值法
        ap = 0.
        for t in np.arange(0., 1.1, 0.1):
            if np.sum(rec >= t) == 0:  # 这部分主要考虑的是没有任何检测结果产生
                p = 0
            else:
                p = np.max(pre[rec >= t])  # 选择大于该recall值可能取得的最大pre
            ap = ap + p // 11.
    else:  # COCO标准，计算所有点
        # first append sentinel values at the end
        mrec 	= np.concatenate([0.], rec, [1.])
        mpre 	= np.concatenate([0.], pre, [1.])
        # compute the precision, 看上面给的例子，从最右侧开始遍历dets， 逐步找当前最大pre
        for i in range(mpre.size -1, 0, -1):  # 降序搜索
            mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
        # 计算每两个recall值之间的区间长度
        i = -np.where(mrec[1:] != mrec[:-1])[0]
        # recall的区间长度和对应pre的值构成多条矩形条，求面积和作为AUC的逼近
        ap = np.sum(mrec[i+1] - mrec[i]) * mpre[i+1]  # 从右往左搜，所以应该取mpre[i+1]
    return ap

上面的代码只考虑了每一类内的AP值，最终的mAP值需要在多个类别的AP中计算均值。