深度学习-nms 和 softnms [代码]

NMS ( Non-Maximum Suppression), 非极大值抑制算法，在目标检测领域内非常常见。而SoftNMS是针对于NMS提出的进一步改进。本文主要阐述NMS和SoftNMS算法并分享其代码实现。

NMS

NMS的大致思想是对于发生重叠的候选框通过选择最大置信度的候选作为最终候选的同时，抑制与该候选重叠度较大的其他候选框。这种做法的motivation在于，如检测器这种模型，对于一个目标可能检测出多个重叠度的响应，而这些相应置信度都挺高，不能简单的通过阈值处理，毕竟阈值是全局的很难统筹各种情形，这时候就希望从多个中选择一个然后将其他候选抑制掉。

其实按照这个思想，不同的问题可能有不同的变种，比如非最小值抑制、非中值抑制等等，

NMS的具体步骤：

S1. 将所有的候选框按照置信度降序排列。选择置信度最高的候选框，认为是正确的检测框。

S2. 遍历剩下的所有候选框，将那些与最高置信度检测框的重叠度大于阈值的候选框删除。

S3. 从未处理的候选框中重新选一个最高置信度的候选框，认为是正确检测框。

S4. 重复S2-S3, 直到所有的候选框都被处理过，保留下来的检测框就是最终的检测结果。

python代码

import numpy as np
def py_cpu_nms(dets, thresh):
    """ nms 
    params dets: 	array, detections, N x 5
    thresh: 		float, iou thresh
    """
    x1, y1, x2, y2 = dets[:, 0], dets[:, 1], dets[:, 2], dets[:, 3]
    scores 	= dets[:, 4]
    
    areas 	= (x2 - x1 + 1) * (y2 - y1 + 1)  # 每一个box的面积，用于后续IoU计算
    order 	= np.argsort(-score)  # 所有的候选框按置信度降序排列
    keep 	= []  # 保存最终留下来的候选框的索引
    while order.size > 0:
        ind = order[0]  # 当前最大置信度的候选框的索引
        keep.append(ind)
        # 接下来计算其余的未处理候选框与当前最可信候选框的iou
        ref = dets[ind]
        can = dets[order[1:]]
        xx1 = np.maximum(ref[0], can[:, 0])
        xx2 = np.minimum(ref[2], can[:, 2])
        yy1 = np.maximum(ref[1], can[:, 1])
        yy2 = np.minimum(ref[3], can[:, 3])
        
        w 	= np.maximum(0., xx2 - xx1 + 1)
        h 	= np.maximum(0., yy2 - yy1 + 1)
        inter = w * h
        union = areas[ind] + areas[order[1:]] - inter
        iou = inter / union
        
        # 剔除与当前候选框的重叠度大于阈值的框
        inds = np.where(iou <= thresh)[0]
        order = order[inds + 1]  # 剩下未处理的候选结果，依然是降序排列的
        # 注意这里在gather order时，inds需要加1是因为 iou计算是计算个数比order个数少1， 也就是order中的第一个没有参与运算， 如果上面计算iou时，使用的是can = dets[order], 那么这里不需要加1，那样的话极限条件比如thresh=1.1时就会死循环
    return keep

Soft NMS

NMS的贪心算法存在一些问题。如下图所示，黑色框和绿色框都是当前候选框，置信度分别为0.9和0.8，按照NMS操作肯定会选择红色框，然后红色框会把绿色框抑制。但是绿色框其实对应着其他的目标，只是两个真实的目标重叠度较大。另外NMS的阈值也不好确定，因为可能处于不同区域，不同遮挡程度的场景中对应的阈值也不同，很难设置一个较好的全局的阈值。

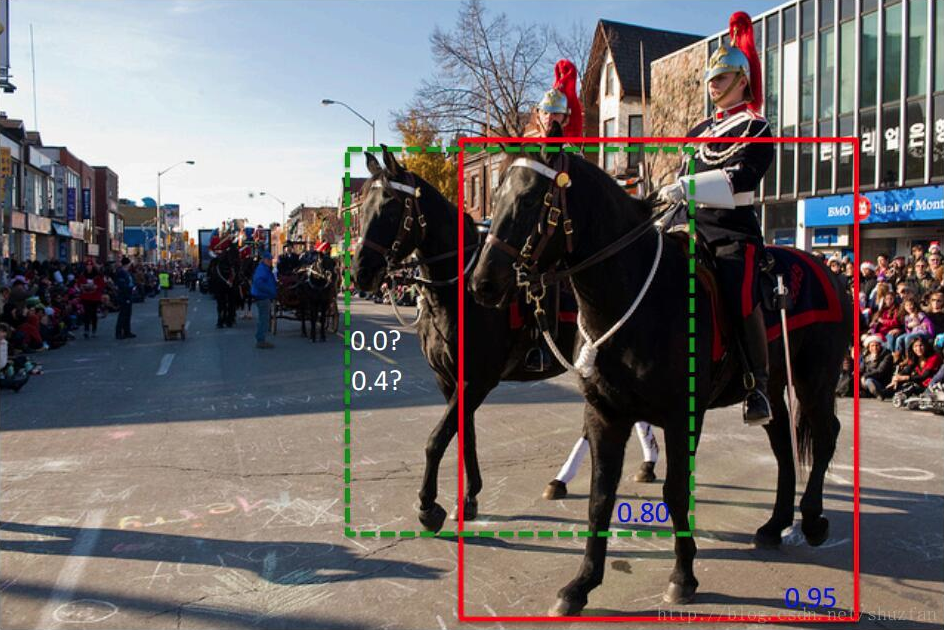
candiates

来源：https://blog.csdn.net/shuzfan/article/details/71036040

基于以上原因， SoftNMS被提出来。 SoftNMS认为NMS过于暴力，只要是与高置信度的候选重叠度大就直接被抑制掉没有回旋空间。所以SoftNMS不是硬性的抑制非最大值，而是给非最大值一定的衰减空间。其伪代码如下：

softnms

可以发现softnms 和NMS的区别只是在于选择了一个高置信度候选之后剩下的框怎么办？

NMS是将IoU大于阈值的剔除，而SoftNMS则是给剩下的候选框一个和iou相关的衰减系数。

$s_i = \begin{cases} s_i & \text{iou} (\mathcal{M}, b_i) \le N_t,\\ s_i(1-\text{iou}(\mathcal{M}, b_i)), &\text{else} \end{cases}$

或者衰减系数也可以是高斯加权

$f(\text{iou} (\mathcal{M}, b_i)) = e^{-\frac{\text{iou} (\mathcal{M}, b_i)^2}{\sigma}}$

python代码, 这里我们模仿nms的代码实现，原始的代码是包含了排序在里面，我们这里直接调用numpy中的函数，想看源码的见softnms github

import numpy as np
def soft_nms(dets, sigma=0.5, Nt=0.1, threshold=0.001, method=1):
    areas = (dets[:, 2] - dets[:, 0] + 1) * (dets[:, 3] - dets[:, 1] + 1)
    keep  = []
    score = dets[:, 4]
    ind = range(len(dets))
    while len(ind) > 0:
        ind_array = np.array(ind)
        tscore = score[ind_array]
        i = np.argmax(tscore)
        keep.append(ind_array[i])
        # 计算与当前候选的iou
        ind = ind.remove(i)
        left_ind_array = np.array(ind)
        tmp = dets[left_ind_array]
        xx1 = np.maximum(dets[ind_array[i], 0], tmp[:, 0])
        xx2 = np.minimum(dets[ind_array[i], 2], tmp[:, 2])
        yy1 = np.maximum(dets[ind_array[i], 1], tmp[:, 1])
        yy2 = np.maximum(dets[ind_array[i], 3], tmp[:, 3])
        
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        union = areas[ind_array[i]] + areas[left_ind_array] - inter
        iou = inter / union
        
        decay_ind = np.where(iou>Nt)[0]
        if method == 1:  # 线性
            score[left_ind_array[decay_ind]] *= (1 - iou[decay_ind])
        elif method == 2:  # 高斯
            ov = iou[decay_ind]
            score[left_ind_array[decay_ind]] *= np.exp((-ov * ov)/ sigma)
        else: 		# original NMS
            score[left_ind_array[decay_ind]] *= 0
         ind = [i for i in ind if score[i] >= thresh]
    return keep

虽然实验证明了softnms效果比nms效果好一些，但是softnms同样需要阈值，以确定哪些重叠框需要乘上衰减系数。