归纳总结-梯度消失和梯度爆炸

梯度消失和梯度爆炸产生的原因

mlp

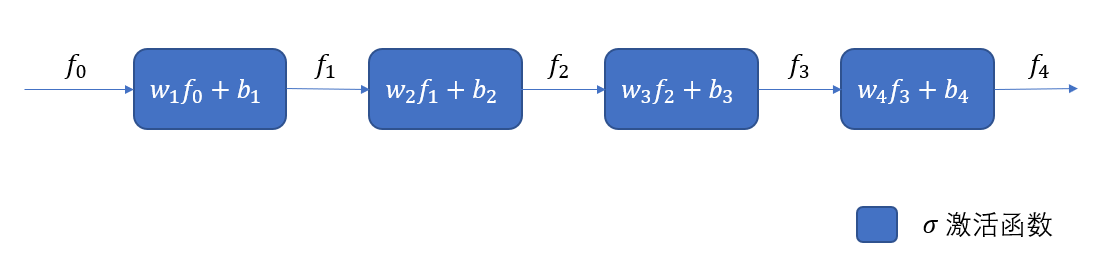
我们以简单的多层感知机为例，已知该MLP的层数为k=4， $f_i = \sigma(w_if_{i-1}+b_i), i=1,2,\cdots,k$ 表示第i层的非线性变换，$\sigma$表示激活函数主要用来非线性变换，$w_i, b_i$分别表示第i层的待学习的权重和偏置, $f_0$表示网络的输入。损失函数可以使用$L(f_k, y)$表示，其中$y$是ground truth。于是整个网络可以表示为如下的映射

$f_k = \sigma(w_k f_{k-1} + b_k)$

所谓的梯度反传就是计算损失函数在每一个需要利用梯度更新数值的变量上计算偏导。
对第$k$层的$w_k, b_k$计算偏导数可以得到：

$\begin{aligned} \frac{\partial L}{\partial w_k} &= \frac{\partial L}{\partial f_k}\frac{\partial f_k}{\partial w_k} \\ &= \frac{\partial L}{\partial f_k}\frac{\partial \sigma}{\partial(w_k f_{k-1}+b_k)}f_{k-1} \\ \frac{\partial L}{\partial b_k} &= \frac{\partial L}{\partial f_k}\frac{\partial \sigma}{\partial (w_k f_{k-1}+b_k)} \end{aligned}$

对第$k-1$层的偏导数可以计算：

$\begin{aligned} \frac{\partial L}{\partial w_{k-1}} &= \frac{\partial L}{\partial f_{k-1}}\frac{\partial f_{k-1}}{\partial w_{k-1}} \\ & = \frac{\partial L}{\partial f_k} \frac{\partial f_k}{\partial f_{k-1}}\frac{\partial f_{k-1}}{\partial w_{k-1}} \\ & = \frac{\partial L}{\partial f_k}\frac{\partial \sigma}{\partial(w_k f_{k-1}+b_k)}w_k\frac{\partial f_{k-1}}{\partial w_{k-1}} \\ & = \frac{\partial L}{\partial f_k}\frac{\partial \sigma}{\partial(w_k f_{k-1}+b_k)}\frac{\partial \sigma}{\partial(w_{k-1} f_{k-2}+b_{k-1})}f_{k-2}w_k \\ \\ \frac{\partial L}{\partial w_p} &= \frac{\partial L}{\partial f_k} \frac{\partial \sigma}{\partial(w_k f_{k-1}+b_k)} f_{p-1} \prod_{i=p}^{k-1}\frac{\partial \sigma}{\partial(w_i f_{i-1} + b_i)}w_{i+1} \end{aligned}$

于是我们发现第 $p, p<k$层参数的梯度和 $\delta_i = \frac{\partial \sigma}{\partial(w_i f_{i-1} + b_i)}w_{i+1}, i=p, \cdots, k-1$有关，若每一个因子$\delta_i$都小于1，则乘积趋于0；若每个因子都大于1，则乘积趋于无穷大. 那么什么情形对导致因子 $\delta_i$过小或者过大呢？$\delta_i$与激活函数的导数和后面层的权重参数有关。所以深层网络产生梯度消失和梯度爆炸有两个原因：激活函数不合适、权重参数出现问题。

激活函数不合适：

以sigmoid函数为例：

$\sigma(x) = \frac{1}{1+e^{-x}}$

其导数为：

$\sigma'(x) = \frac{e^{-x}}{(1+e^{-x})^2}$

其曲线图如下：

import numpy as np
import matplotlib.pyplot as plt
s = lambda x: 1/(1+np.exp(-x))
ds = lambda x: np.exp(-x)/(1+np.exp(-x))**2
plt.subplot(121)
plt.plot(x, s(x))
plt.title('sigmoid')
plt.subplot(122)
plt.plot(x, ds(x))
plt.title('ds')
plt.show()

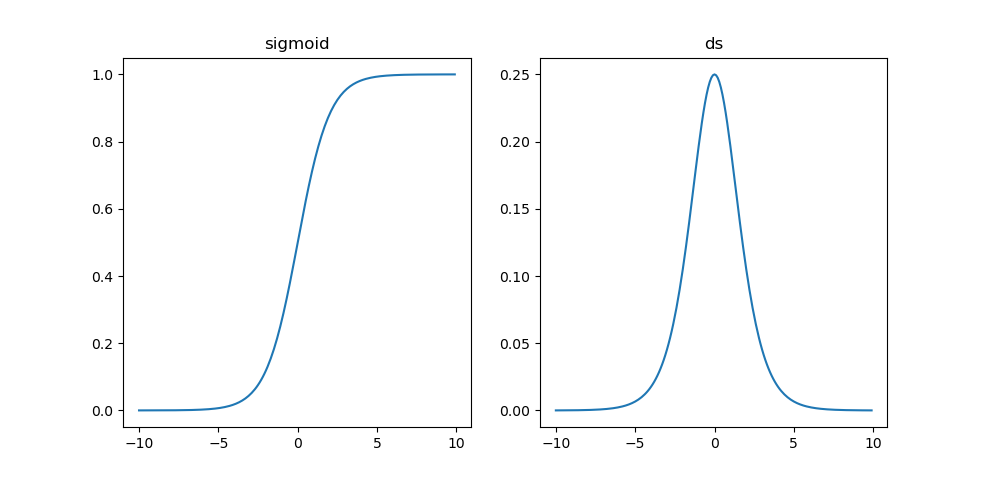
sigmoid and its gradient curve

可以发现sigmoid函数的最大梯度值$\sigma’(x)$在0点取得， $\sigma’(0)$ = 1/4, 而网络权重初始化时一般能保证$|w| < 1$,所以这样就使因子$\delta_i$小于1，对于太深的网络层参数的偏导数趋近于0，即$\Delta w_p = 0$, 而梯度下降法的迭代公式是: $w^{t+1}_p = w^{t}_p - \eta\Delta w_p$, 也就是说这是更新不动参数，称之为梯度消失了。

如果网络初始化不合适的话，可能随着迭代次数的增大，权重$w_i, i=p,\cdots,k$一直增长的很大，这时候就可能导致因子$\delta_i$太大，从而溢出，也就是网络训练过程中会出现 nan 的原因。

避免梯度消失和梯度爆炸的方法

对症下药：

使用其他的激活函数，比如ReLU函数:
$ReLU(x) = \begin{cases} x, \text{ if } x>0;\\ 0, \text{ else} \end{cases}.$
可以发现，对于ReLU函数，其正值部分的偏导为常数1，因此连乘对其没影响，缓解了梯度消失现象。
梯度截断/正则。既然梯度过大可能导致权重更新过大进而导致梯度爆炸，那就对梯度进行截断，避免权重突然变得很大。梯度阶段还能避免每次更新步长太大收敛不稳定。
微调。我们也提到权重的初始化也有可能导致梯度消失或爆炸，那么在预训练权重上进行微调有助于选择合适的权重参数，避免梯度消失或爆炸。
跨层连接。即ResNet结构, 梯度消失和爆炸是由于层数太多，导致乘数因子个数太多，那么通过跨层连接能够减小每一层的最小深度。
BatchNorm。批量归一化的目的是让每一层的输入拉到相似的分布区间内，避免有些层分布区间太大，导致激活函数的导数趋于0.
LSTM结构。 LSTM结构通过多种门能够保留更长的历史信息，反过来误差反传时也能保存更多的误差信息，我觉得这个和跨层连接的原理是相同的，只是具体实施的时候不同，LSTM会对误差进行变换后前传，而skip-connectiion直接跨层反传的就是误差。